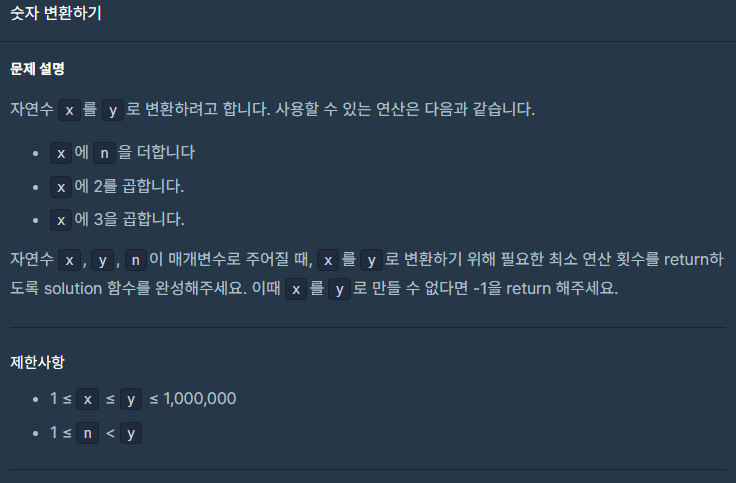
이 문제는 숫자 변환에 관한 것입니다.
주어진 조건에 따라 x+n, x*2, x*3이 실행되며 목표 수 y로 변환하기 위한 최소 연산 수를 달성해야 합니다. x를 y로 변환할 수 없으면 -1을 반환해야 합니다.
세 가지 작업을 사용할 수 있지만 순서가 없으며 하나만 사용하는 것은 관련이 없습니다.
주어진 연산을 x에 적용하여 y를 생성하거나 y에 주어진 연산의 역수를 계산하여 x를 생성하는 두 가지 방법이 있습니다.

내가 생각한 해결책은 y에 연산을 적용하는 것이었다. 이 방법을 선택한 이유는 어차피 골이 가능한 방법을 찾기 위함이고, x를 기준으로 한다면 불필요한 계산이 더 많아진다.
x가 15, y가 50, n이 10이라고 가정합니다.
처음 3개의 연산을 적용하면 x = (30,45,25)가 됩니다.
그리고 각 원소를 기준으로 다시 연산을 하면 ((60, 90, 40), (90, 135, 55), (50, 75, 35))가 된다.
눈으로 바로 찾을 수 있지만 코드로 다시 찾으면 먼저 40을 검색한 다음 50을 찾아 계산 횟수 50을 반환합니다.
반대로 y를 기준으로 계산하면
첫 번째 작업에서 두 개(25.40)만 나옵니다. 50은 3의 배수가 아니므로 2로 나누고 10을 빼는 두 가지만 확인하면 됩니다.
25는 2와 3의 배수((15), (20, 30))가 아니므로 이 두 요소에 대해 총 3개의 경우가 도출된다.
세 번째 연산((5,5),(10,10),(15,10,20))에서도 조건에 따라 ((10,10),(15,10,20)) 만 남습니다.
코드는 pop()을 사용하므로 더 빠르게 작업하려면 deque 라이브러리를 사용하는 것이 좋습니다.